Contents
特徴量エンジニアリングとは?
特徴量エンジニアリングとは、機械学習モデルのパフォーマンスと精度を人為的に向上させるために有効な、新たな特徴量 (変数) を作成する作業のことです。
予測精度に大きく寄与する有用な特徴量を作れるかどうかによって、最終的に構築される機械学習モデルの精度の成否を大きく左右されます。同じ目的で開発したモデルでも、予測精度が低ければ利用価値はありません。より利用価値の高いモデルを作るためには、人が意識的にモデルの精度を上げることができる特徴量エンジニアリングが不可欠です。
表形式のデータを用いた特徴量エンジニアリングにおいて、経験的には専門領域のドメイン知識を利用した特徴量が極めて効果的といわれています。なぜなら、分析対象の分野に専門知識があればあるほど、データに存在する各特徴量に対して造詣が深くなり、それらの関係性を容易に発見・想定し、深く理解することができるからです。結果として、複数の関係性が深い特徴量から、有意義な特徴量を新たに作成できるはずです。
精度の高い人工知能を実現するためには、いかに優れたデータを集め上手に加工できるかが特徴量エンジニアやデータサイエンティストにとってのとっておきの腕の見せどころでしょう。
特徴量エンジニアリングが重要な理由
機械学習モデルを構築する際の中核的な存在はデータであり、取り扱うデータによって特徴量エンジニアリングのやり方にさまざまな工夫が必要となります。
特徴量エンジニアリングが重要な最たる理由は、この特徴量エンジニアリングの工夫の仕方・テクニックによって、機械学習における予測精度の優劣が大きく左右されるからです。
しかし、 特徴量エンジニアリングが重要な理由はこれだけではありません。
それ以外の理由として、以下で2点の理由について説明します。
理由1 : 分析対象のデータや分野の造詣が深まる
特徴量エンジニアリングは、非常に価値の高いデータサイエンスのテクニックの1つですが、モデルの精度向上に有効な新たな特徴量を生み出すことができれば、データに対する理解が深まり、データ分析の視界が広がります。前の章で、「 分析対象の分野に専門知識があればあるほど、データに存在する各特徴量に対して造詣が深くなり、それらの関係性を容易に発見・想定し、深く理解することができる 」と述べましたが、この逆も然りということです。
つまり、有効な特徴量エンジニアリングを行うために、データと真正面に向き合い、データの関連性について思考するという過程が生じることで、分析対象のデータや分野に明るくなっていくということです。
理由2 : 正しく実行すれば非常に価値が高い
特徴量エンジニアリングの最大の目的はモデル精度の向上ではありますが、それ以外にも複数の目的があります。例えば、機械学習の処理速度の高速化・結果の理解や解釈の容易化・過学習の防止などがあります。
機械学習が正しく実行できなければ、データに存在するノイズによってむしろ精度を落とすこともあるため、有効な特徴量を正確にエンジニアリングしてノイズを除去することが重要です。
特徴量エンジニアリングの代表的手法
新しい変数を作る特徴量
既存のデータの表 (行列) に、新しい変数 (列) を追加する形で作成されます。
大きく分けると、単体の変数だけから作成できる特徴量と、複数の変数を組み合わせて作成する特徴量の2種類に分けられます。
単体の変数だけから新たな特徴量を作成する方法には、 対数、べき乗、離散化、スケーリング (正規化・標準化) 、 ロジット変換、 ダミー変換 (Encoding) 、 二値化、差分などがあります。
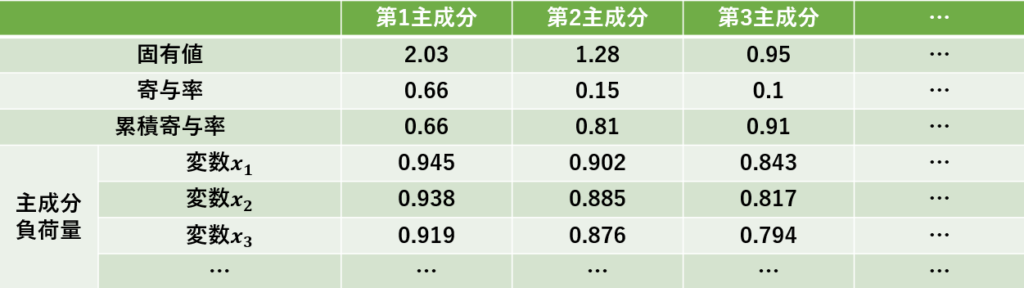
一方、 複数の変数を組み合わせて特徴量を作成する手法には、四則演算 (交互作用) 、 特異値分解 (主成分分析) 、 距離、 クラスター分析、ニューラルネットワーク (ディープラーニング ) などがあります。
複数のサンプルから作る特徴量
グループ毎の平均値や標準偏差を算出するというなじみのある作業も、この作り方に当てはまります。 例えば、毎日の最高温度のデータを月毎に集計したり、学年全体のテストの成績から、全体の平均点や各生徒個人の偏差値 ( (自分の得点-平均点) ÷標準偏差×10+50) を求めたりすることなどが、複数のサンプルから新たな特徴量を生み出している例として挙げられます。 この集計は、 Excelのピボットテーブルや、各種BIツールの主要な機能にもなっています。
この手法も大きく2つに分けることができます。分類基準としては、時間軸 (時系列データ) がある場合と時間軸がない場合です。
時間軸がある場合の手法としては、ラグ (遅延) や移動平均、最大、最小、分散、自己共分散などが挙げられます。
対して、はじめに例として挙げた気温や成績データのように時間軸が無い場合の手法には、カテゴリー毎や階級毎の平均、分散、最大、最小などがあります。
階級ごとやグループごとに集計する場合、生データよりも標本数 (データの行数) が減ることが大多数です。
数学的な空間を変えて作る特徴量
数学的な空間自体を変換します。 生データとは、列の名前も全く異なるものになります。
この手法の代表例として、フーリエ変換がよく知られています。




コメントする