因子分析とは

因子分析は「多変量解析」の分析手法の一つであり、数多くの変数を少数の潜在変数（因子）に要約してまとめることで、それらの変数がどのような潜在的変数によってどの程度影響を及ぼされているのかを探る分析手法です。いくつかの変数が相互に高い相関を持つとき、それらの変数は何か共通のものを測定していると考えられます。この観測されたデータの相関関係から、データに共通して影響を与えている因子を探り、各変数の性質をよりコンパクトな形で記述することが因子分析の目的です。

また、潜在変数（因子）に対する反応の違いから、個々の回答者（ユーザーや属性グループ）の意識・行動や志向性の違いを明確化できます。マーケティングの現場では、アンケート調査の結果を分析し、回答者の「潜在意識」や「目に見えない口コミ評価」といったようなものを見いだす目的で用いられます。具体的には、ある商品カテゴリーのユーザー評価から、購入に結びつく潜在的な評価要因を把握し、自社及び競合他社がそれらの要因に対してどのような位置づけにあるかを明確化します。

マーケティング以外の例としては、例えば、教育分野における各生徒の各教科でのテストの得点から個人の潜在能力を図るといった活用方法が挙げられます。国語のテストと英語のテストに強い相関関係があり、数学と物理の間にも強い相関関係があるとすれば、その背後には言語能力と数的能力という2つの因子があることが推測されます。このように、因子分析は、観測されたデータからその背後にあって直接測定できない要因を推定する手法と言えます。

因子分析の用途・メリット

因子分析の主な活用方法としては、以下のようなものが挙げられます。

• 分析結果を簡潔化して解釈を容易に
  消費者調査のアンケートや顧客満足度といったアンケートの結果を分析する際に、質問項目が多くなりすぎると結果の解釈が困難になることが多々あります。そこで、多数ある変数のうち相関関係 (共通性) の高いものを見つけ、それらに共通していそうな要因を抽出してシンプルにすることで、結果の解釈や新たな知見の考察を容易にすることができます。
  
• 潜在的なニーズを定量的に把握
  競合他社や自社に対して同一の質問項目がある調査を行うことで、主観に依存しない客観的・定量的なニーズの調査が行えます。
  例えば、車の各性能について自社のイメージを評価してもらい、評価軸の数より少数の因子をその評価の中から抽出します。そうすることで得られた「コストパフォーマンス」、「デザイン性」、「機能性」等といった因子に関して、他の属性 (年齢、性別、居住地など) でグループ分けすることで、顧客の潜在的なニーズを理解しやすい形で把握することができます。ある年代に特に強く影響している因子を発見したり (若い世代はデザイン性とコストパフォーマンスを、中年世代は機能性や安全性を重視しているといった) 、年代ごとの重要視している要素を明らかにすることができます。
  また、前の章でも触れたように、競合の各社についても同じ質問項目を同様に消費者に尋ねることで、得られた共通因子から自社及び競合他社のポジショニングマップを作成することもできます。

因子分析に関連する用語解説

• 【因子負荷量】
  直交解を求めた場合に限りますが各変数と各因子の相関を表します。その場合は因子負荷量は、相関係数なので-1～1の値をとります。直交解の方法としてはバリマックス回転がよく利用されます。しかし、次の項の共通性の推定により、独自因子の情報は共通因子空間から除かれていることに注意してください。通常、この因子負荷量が高い変数に注目して、共通因子名を付けます。
  
• 【共通性】
  各観測変数が共通因子によってどの程度説明できているかを割合で表した指標です。割合ですので、0から1の値をとります。0は全く説明できていないことを表し、1は完全に説明できている状態を表しています。これも直交解を求めた場合に限りますが共通性は、各因子負荷量の2乗和となります。

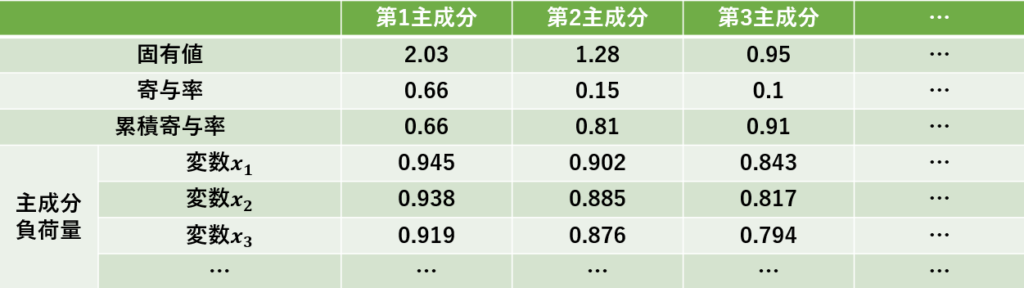
• 【寄与率】
  ある因子がある観測変数に対してどの程度の説明力を持っているか割合を表します。
  
• 【累積寄与率】
  寄与率を左から順に合計した数値。これによって、それまでの因子で全体をどれだけ説明しているかという割合を示します。
  
• 【因子得点】
  因子得点は、各因子ごとの各個体（対象者）のスコアを表します。因子得点が高い人は、その因子に影響されている度合いが高いといえます。計算方法としては、「回帰法」や「バーレット法」などがあります。

因子分析の流れ

因子分析の手順は一般的には次のような枠組みで構成されています。

1. 因子数の決定
   因子の数の決め方は主に二通りあります。一つは事前に因子同士の関係性や数にある程度の仮説があり、その仮説に基づいて因子の数を設定する方法と、もう一つは統計ソフトを使って定量的に因子の数を決定する二つの方法があります。後者の場合は、対象データから統計ソフトで各因子の「固有値」を計算し、各因子をその固有値の大きい順に並び変え、固有値が急激に小さくなる手前までの因子を共通因子として採用します。明確な仮説がない場合は定量的な手法を採用し、具体的にはスクリープロット、MAP基準やBIC基準を用いて因子の数の目安を決めます。共通因子の数を決定する方法は他にもいくつかあります。
   
2. 因子負荷量の推定
   次に共通因子の影響の強さを示す「因子負荷量」を抽出します。その抽出方法は複数存在します。どの抽出方法も統計的に間違いではなく、考え方と計算方法の違いです。その中で最も一般的な抽出方法は「最尤法」です。その他にも「主因子法」、「主成分法」などがあります。このステップで人間が実際に計算することはなく、RやPythonといった統計ソフトを用いて計算を行います。
   
3. 因子軸の回転
   回転とは、因子の解釈を行いやすくするために行うもので、因子負荷量の相対的位置を変えないまま数値に濃淡をつけて解釈しやすい値に置き換えることです。推定した各観測変数の因子負荷量を散布図グラフにすると、そのままでは因子負荷量が大きい値がばらついており、共通因子が何を指しているのかわかりにくく解釈が困難な場合があります。その場合、散布図のグラフの軸を各因子の数値が縦軸と横軸の両方に沿って位置するように回転させることで、因子負荷量それぞれの相対的な位置を保ったまま、具体的な数値をより1や0に近づけ解釈しやすい形にすることができます。因子負荷を推定した際にそのままわかりやすい形であれば回転をしなくても構いません。このステップでも統計ソフトを用いて、数値の変換を行います。その際に用いられる回転の計算方法にも多くの種類がありますが、バリマックス法がよく用いられています。
   
4. 因子の解釈
   因子軸の回転を適宜行いながら、因子負荷行列を解釈しやすい形に整形できたのちに、座標軸を回転させた後の因子のグラフや各因子の因子負荷量を見ながら、各共通因子の解釈とネーミングを行っていきます。これは決まった答えがあるわけではありませんので、分析者の主観になります。自らが「主観的」に決定した答えに、どれだけの「客観性」と「合理性」を持たせることができるのかということも分析者の腕にかかってきます。
   
5. 因子得点の算出
   各アンケートの回答者や回答者のクラスター（階層、グループ）の特徴を分析したい場合は、因子得点を算出します。因子得点によって、共通因子から見た各回答者の能力や資質や好みなどが推測できます。

因子分析の注意点

• 因子の数は人が決定する
  因子分析の流れを説明する際にも言及しましたが、因子の数は人が決めることになります。しかし、この際明確な仮説や基準がないままに因子の数を決定しても分析結果を解釈することが困難になってしまいます。もし明確な仮説がない場合は、定量的な手法を採用し統計ソフトである程度因子数の目安を付けることが重要です。
  
• データの事前準備に注意
  因子分析は相関関係をもとにした分析方法であるため、変数間の相関関係がないデータに関しては因子分析を行っても相関係数に反映されません。また、扱えるデータの型はデータは数的データのみであり、質的データは分析不可能です。共通因子は観測変数より少なくなるため、質問項目は共通因子の目安3～4倍が望ましく、回答者は項目数の5～10倍程度が望ましいと言われています。また、因子分析では4段階、あるいは6段階の評価を利用することが多いです。