Contents
主成分分析とは?
「主成分分析」とは、多次元データのもつ情報をできるだけ損わずに低次元空間に情報を縮約する多変量解析手法の一種です。データの持つ情報量をなるべく元から削ぎ落すことなくかつ全体がわかりやすいように、複数の量的な説明変数を、極力少ない新たな指標や合成変数に要約する手法です。この要約は「次元の縮約」と呼ばれます。要約した合成変数のことを「主成分」と呼びます。
わかりやすく言えば、膨大な次元(指標)のデータから、全体をわかりやすく見通しの良い1~3程度の次元に要約していくことです。もっとわかりやすく説明するために具体例を挙げると、身長と体重という2次元から、BMI(Body Mass Index)という肥満度を表す1次元の指標に要約するといったことが主成分分析とも言えるでしょう。
たとえば、国語・数学・英語・理科・社会の5教科のテストから、個々の生徒の能力を知りたいとします。しかし、そこでテスト結果を分析する際、ある教科の点数と別の教科の点数は単純には比較できません。なぜなら、教科によって平均点も違えば、点数分布 (点数のバラツキ・分散) も違うからです。
このような場合に主成分分析を行うと、第1主成分に総合成績、第2主成分に文系科目/理系科目という指標で、各学生の能力を可視化できます。その結果、ある学生の総合的な学力がどのくらいなのか、文系と理系のどちらの能力が高いのかが一目瞭然になります。このテストの成績の縮約例では、5次元の点数データを2次元の点数データへ縮約していると表現できます。
主成分分析の目的
情報量の多いデータを要約して特徴を可視化する
ビッグデータは3次元を上回るような高次元 (多変量) データがほとんどで、データの構造を可視化することがほぼ不可能なため、データを理解することも困難であることが多いです。しかし、実際には多数の変数間に相関があったり、上質な情報を多く有しているような重要な変数は少なかったりするケースが大抵であるため、「情報を失うことなく変数を減らすことが可能だ」という考えが生まれました。できるだけ情報を失うことなくデータの次元を減らすことを次元削減と呼び、その代表的な手法が主成分分析です。特に、我々が日常生活している3次元以下まで次元を削減することができれば、データ全体の雰囲気の可視化が可能となり、我々のような「ヒト」が理解しやすいデータへと変換されたと言えるでしょう。
主成分分析で得られた主成分をクラスター分析や回帰分析に利用する
- 多重共線性の解決:主成分分析によって作られる新たな変数を主成分と呼びますが、主成分はそれらの定義上互いに独立であるため、主成分を説明変数として回帰分析をする際は、元データでは生じていた多重共線性を気にしなくてもよくなります。
- 新変数の作成:クラスター分析の際には、より縮小された次元を使うことで、少ない計算量で分析を行えるようになります。また、より特徴づけられた変数を使うことになるため結果の解釈が示唆に富んだものとなる場合があります。
主成分分析のアルゴリズム
主成分分析のアルゴリズム (挙動) をまとめると、次のようになります。
- 全データの重心(平均値)を算出
- 重心からデータの分散(ばらつき)が最大となる方向(第1主成分)を算出
- 第1主成分と直角に交わる(直交)方向で分散が最大となる箇所(第2主成分)を算出
- 直近の主成分と直交する方向で分散が最大となる箇所(第3主成分)を算出
- 4をデータの次元分だけ繰り返す
詳しくはこの統計科学研究所が作成した主成分分析の解説pdfをご参照ください。アルゴリズムを図で説明しているだけでなく、主成分分析とはといった導入から関連用語、統計解析ソフトRを用いた実装方法まで詳しく記載されています。
主成分分析の結果とその解釈方法
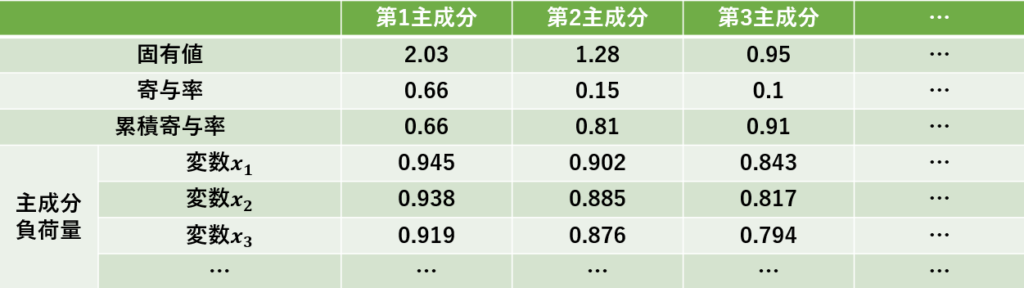
以下では、上表に記載されている主成分分析を理解するのに必要な専門用語の説明を行っていきます。
- 固有値 : 固有値とは各主成分が含んでいる情報の大きさを示す指標です。一般的には、固有値が「1以上」ある主成分が、元のデータとの関連が深いとされています。
- 寄与率 : 寄与率とは、この主成分だけで元のデータをどれほど説明することができているかを表した数字です。今回の場合、第1主成分で元データの66%までを説明できていることになります。要約すると必ず漏れてしまう情報があり、そのために第2主成分以降が必要となります。第i主成分の寄与率は、第i主成分の固有値を総分散で割ることで求められます。
- 累積寄与率 : 第2、第3と続く主成分の各寄与率を足した数値です。一般的に累積寄与率が80% (もしくは90%) 以上となるまでの主成分を新たな変数として分析に用います。今回の場合、第2主成分で初めて80% (閾値が90%の場合は第3主成分まで) を超えたので、ここまでを分析対象とします。第i主成分までの累積寄与率は、第i主成分までの固有値の総和を総分散で割ることで求められます。
- 主成分負荷量 : 元データの各変数(数値)に対して与えられる係数です。この数値の絶対値が大きいほど、各変数が主成分にもたらす影響力が大きいことを表します。また、符号の正負によって、その変数が与える影響の向きが決定されます。
主成分分析の注意点
主成分得点の解釈は自分で行う
主成分得点とは、元データの各変数を合成した変数となる各主成分を軸とした場合の各変数の得点であり、基本的にはz=a1x1+a2x2+…+anxnという数式の形で表されます。主成分は分析に用いた変数の数だけ出来上がります (元の変数がn個なら、新たに生成される主成分もn個となります) が、通常、2つの主成分をそれぞれ縦軸と横軸に取った散布図を作成して分析作業を行います。得られた散布図により各変数の位置関係が可視化されることで、それぞれの変数の特徴を把握することが可能となります。それぞれの主成分得点がどのような意味を持つかは、係数の値に注目して人間が解釈する必要があります。この解釈こそが、データサイエンティストの手腕の見せ処と言えるでしょう。
主成分分析自体が目的になることはほとんどない
主成分分析は人間にとってわかりやすいデータを構築するための手法の1つです。回帰分析のように、売上や利益に直接影響する要因やその影響の大きさを推定するわけではありません。クラスター分析や回帰分析、その他の多変量解析を行う前段階のデータ整形のための分析といえます。そのため、主成分分析はビジネスの場面で使われることはほとんどなく、データ分析の実務で使われることが多くなる分析方法です。
主成分分析を用いるケース
主成分分析はマーケティングや研究開発など、様々な分野で現在用いられています。例えば、以下のようなケースで用いられることが特に多いです。
●アンケート調査の結果分析
主成分分析で最も多い活用法は、顧客満足度調査やブランドイメージ調査、利用者調査などのアンケート結果の分析でしょう。数多くの質問に対する顧客の回答データを主成分分析し、総合評価を出したり、顧客が重視している点を推測したりするといった使い方です。さらに、主成分得点を基に顧客セグメントがどういう嗜好なのかというポートフォリオを作成したり、第2主成分以降の内容から顧客が評価している軸を探って商品開発に活かしたりといった活用も進んでいます。
●メディアの企業や商品評価
新聞やテレビなどのメディアで掲載される企業ランキングは、一般的には主成分分析での総合指標によって評価されています。たとえば日本経済新聞の環境経営度調査や品質経営度調査でも、主成分分析の主成分によるランキングが採用されています。
●研究開発
研究開発は数多くの材料を使って実験を行い、膨大なデータが蓄積されていきます。それを分析する際にも主成分分析が使われます。たとえばお酒造りの際、さまざまな酵母をさまざまな条件で試した実験結果を主成分分析すると、総合点の他に、酵母のどういう特性が存在するか、また他の多変量分析と合わせてどの特性がお酒の味に好影響を及ぼすのかを推測できるようになります。
●画像処理
画像補正技術にも応用されています。解像度の低い画像をきれいな画像に修正する際や拡大する際に、粗い部分の周辺にある色情報から、どの色を間に加えれば自然な画像になるかを決定します。




コメントする