記述統計とは、統計の手法のひとつで、与えられたデータがどのように分布しているかを検討するために表やグラフを表示し、データの示す傾向や性質を把握する手法のことである。
では、早速Rに用意されているデータセットを使用し、記述統計をしてみる。
今回、使用するデータセットは、”iris”(アイリス) と呼ばれるものである。
アイリスとはアヤメ科アヤメ属の植物で、データセットにはアイリス3種のそれぞれから50の花に対して、それぞれ、がく片の長さと幅と花弁の長さと幅の変数のセンチメートル単位で測定結果が得られる。
まずは実際にデータを確認する。Rの画面で”iris”と入力。以降、150行表示され、Speciesの列にsetosa、versicolor、virginicaの3種類があることが確認できる。

Rでは、$(ドルマーク)の後に列名を書くことで列を指定して出力できる。
iris$Sepal.Length
![]()
それでは、始めにSepal.Length(がく片の長さ)の平均を計算する。そのために平均を計算するmean()関数を使用する。
mean(iris$Sepal.Length) と入力する。
![]()
meanは英語で平均値を意味する”the mean”から来ている。
同様の要領で、標準偏差、分散、中央値、最小値、最大値、範囲を出力する。
それぞれ、sd()、var()、median()、min()、max()、range()関数を使用する。

また、summary(iris$Sepal.Length)と入力すると、最小値、第一四分位数、中央値、平均値、第三四分位数、最大値を一度に出力できる。
![]()
視覚的に確認するためにboxplot()関数を使用して箱ひげ図を表示させる。
boxplot(iris$Sepal.Length) と入力する。
![]()
すると別ウィンドウで画像が表示される。

ここまでirisデータのsetosa、versicolor、virginicaの3種類の全ての合算で計算してきたが、それぞれの種類に対して、記述統計を行う。
subset()関数を使用して必要なデータをだけを取得する。
subset関数の使用方法はsubset(データ,条件式)のように記述する。
具体的にsetosaだけ取得するには以下のようになる。
subset(iris,Species==”setosa”)
今回の場合はSpeciesの列から値がsetosaのものだけを抽出している。
実際に実行してみると、確かにSpeciesの列の値がsetosaの行だけが抽出されていることがわかる。
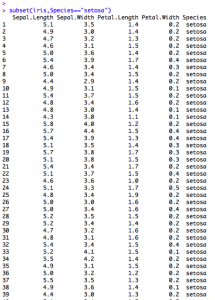
このデータに対して先ほどと同様にSepal.Lengthに対して箱ひげ図を出力してみる。
その際に、boxplot(subset(iris,Species==”setosa”)$Sepal.Length)と記述しても出力できるが、
一度、条件抽出したデータを以下のように、他の変数(今回はsetosaという変数)に格納してから箱ひげ図を出力させる方法もある。
setosa <- subset(iris,Species==”setosa”)
boxplot(setosa$Sepal.Length)
setosa、versicolor、virginicaそれぞれで実行することで、それぞれの種類の特徴が視えてくる。



コメントする