重回帰分析とは、1つの目的変数 (従属変数) を複数の説明変数 (独立変数) で予測しようという分析手法である。多数の説明変数（独立変数）と1個の目的変数（従属変数）の間に適当な直線の式をあてはめることで、目的変数の変動が各説明変数の変動によってどの程度影響されるのかを分析する手法です。このとき、あてはめる式を重回帰式と呼び、この式は最小二乗法により求められる。p個の説明変数がある場合の重回帰式は以下のように表される。

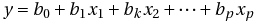
定数b₁, b₂, …, b_pを偏回帰係数といい、各説明変数が1単位変動する毎に目的変数に与える影響量を示している。b₀は定数項を、x₁, x₂, …, x_pは説明変数を、yは目的変数をそれぞれ表している。

多重共線性

重回帰分析を行う上で気を付けなければいけないのが、多重共線性である。多重共線性とは、説明変数の中に、相関係数が高い変数の組み合わせがあることを指す。多重共線性が観測される場合、偏回帰係数の解釈が難しくなるため、相関の強い変数のいずれか一方を除いて再度分析を行い直す方が良いとされている。